The Parallel Lines Cut by Two Transversals Worksheet is an indispensable resource for students seeking to master the intricacies of this fundamental geometry concept. Through a series of engaging exercises and thought-provoking problems, this worksheet empowers learners to grasp the properties and applications of parallel lines intersected by transversals.
Delving into the depths of geometry, the worksheet explores the relationships between alternate interior angles, corresponding angles, and alternate exterior angles. By examining these relationships, students develop a comprehensive understanding of the geometric principles governing parallel lines and transversals.
Parallel Lines Cut by Two Transversals
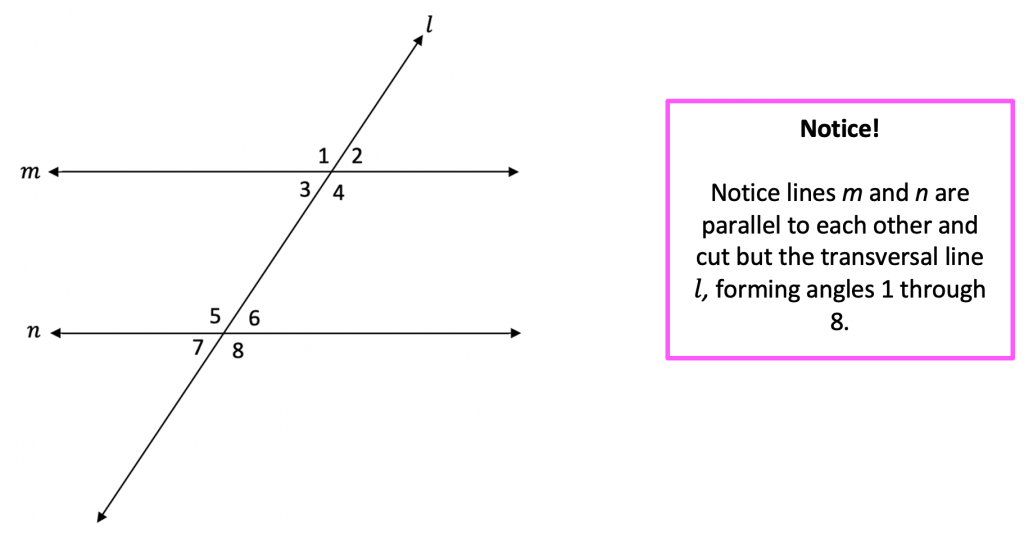
Parallel lines are lines that lie in the same plane and never intersect. Transversals are lines that intersect two or more other lines.
Definitions
Parallel linesare lines that lie in the same plane and never intersect. Transversalsare lines that intersect two or more other lines.
Properties of Parallel Lines Cut by Transversals
When two parallel lines are cut by a transversal, the following properties hold:
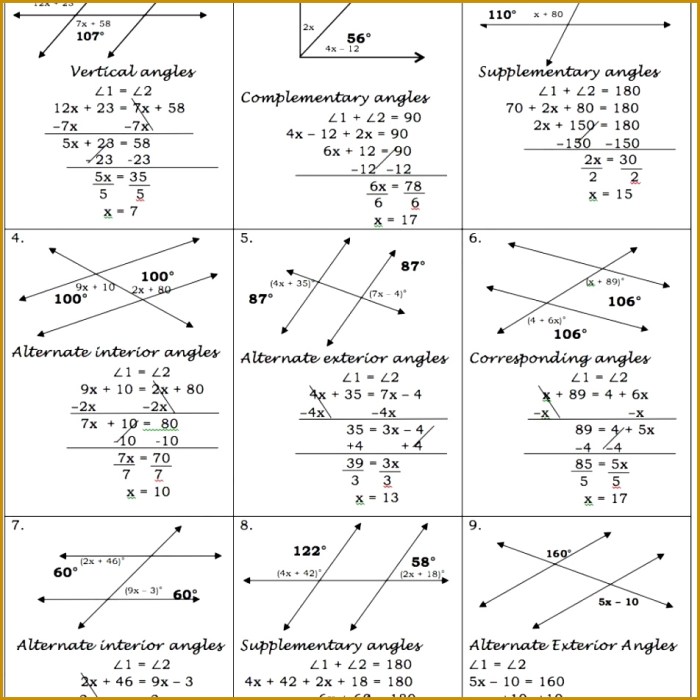
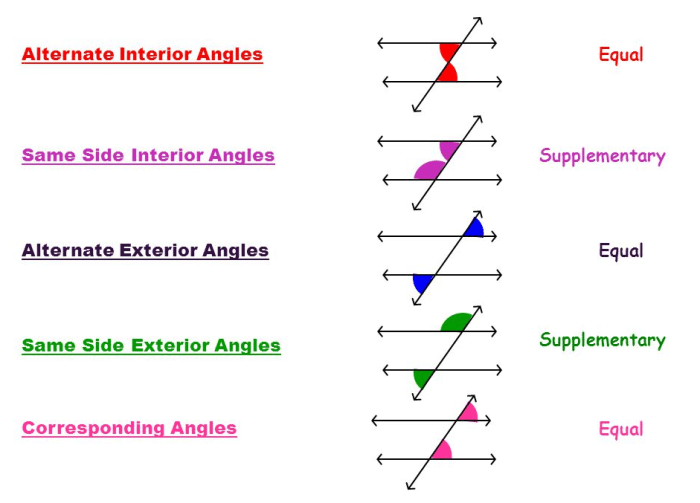
- Alternate interior anglesare congruent.
- Corresponding anglesare congruent.
- Alternate exterior anglesare congruent.
Solving Problems, Parallel lines cut by two transversals worksheet
To solve problems involving parallel lines cut by transversals, use the following steps:
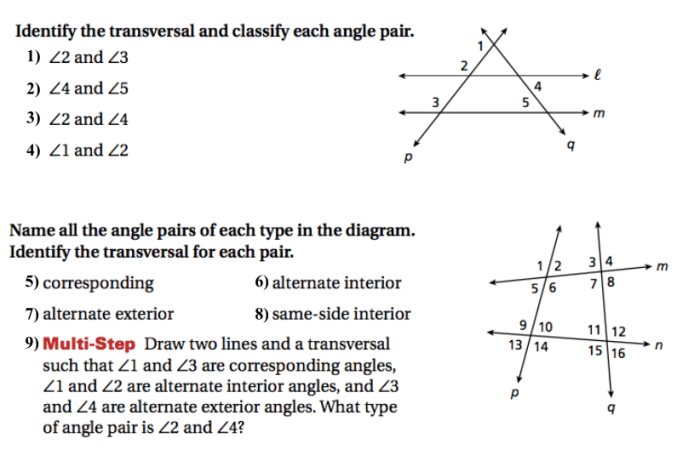
- Identify the parallel lines and the transversal.
- Label the angles formed by the intersection of the lines.
- Use the properties of parallel lines cut by transversals to find the unknown angles.
Applications
The properties of parallel lines cut by transversals are used in many real-world applications, including:
- Architecture: To design buildings with parallel walls and perpendicular roofs.
- Engineering: To build bridges and other structures that use parallel beams.
- Design: To create patterns and designs that use parallel lines.
Practice Problems
Worksheet with practice problems involving parallel lines cut by transversals:
- Find the value of x in the diagram.
- Prove that the lines are parallel.
- Use the properties of parallel lines cut by transversals to find the missing angles.
Visual Aids
Diagram to illustrate the concepts of parallel lines cut by transversals:

Extensions
Advanced topics related to parallel lines cut by transversals include:
- The slope-intercept form of a line.
- The midpoint formula.
User Queries: Parallel Lines Cut By Two Transversals Worksheet
What is the definition of a transversal?
A transversal is a line that intersects two or more other lines at distinct points.
What is the relationship between parallel lines and transversals?
When a transversal intersects two parallel lines, it creates eight angles. The properties of these angles are governed by the relationships between parallel lines and transversals.
How can I use the properties of parallel lines cut by transversals to solve problems?
By understanding the relationships between the angles formed when a transversal intersects parallel lines, you can use properties such as the alternate interior angles theorem and the corresponding angles theorem to find unknown angles and solve geometry problems.